Наименьшее общее кратное чисел: правило как найти и пример задачи с применение НОК

Перед изучением дробей в школьной программе 5 класса по математике изучают тему наименьшего общего кратного, или сокращенно НОК. В рамках наших статей мы даем не только определение и правила нахождения подобных вещей, но и обязательно на практических примерах показываем где это можно применить.

Итак, давайте начнем с понятия. Что такое НОК? Наименьшее общее кратное чисел X и Y равно наименьшему целому числу, на которое делится без остатка эти самые X и Y.

• Найдите наименьшее общее кратное чисел перед операцией сложения или вычитания дробей
• Правило нахождения НОК
• Задача с применением НОК

Найдите наименьшее общее кратное чисел перед операцией сложения или вычитания дробей

Материал вычисления НОК в курсе школьной программы 5 класса не просто так дается перед изучением дробей. Дело в том, что таких операциях с дробями как сложение или вычитание необходимо каждое дробное число привести в общему знаменателю.

Для простоты усвоения материала начнем определять НОК для пары целых натуральных чисел в пределах таблицы умножения. К примеру, есть два числа 6 и 16. Если действовать методом подбора, то можно легко найти наименьшее число, на которое делятся 6 и 16. Это число будет равняться 48. Однако, такой метод подбора касается только простых чисел. А что если необходимо найти НОК для чисел за рамками таблицы умножения. Оказывается в таких случаях есть методика нахождения.

Правило нахождения НОК

Правило нахождения наименьшего общего кратного ряда чисел можно представить в виде следующего алгоритма:

1. Раскладываем каждое число на простые множители.
2. Далее из каждого ряда разложенных чисел выписываем числа, которые имеют общие значения.
3. Из тех чисел, которые присутствуют в каждом разложенном ряде выписываем лишь те, которые имеют наибольшую степень.
4. Производим умножение чисел в соответствующих степенях.

В качестве примера вычисления НОК по данному правилу возьмем два числа 14 и 16.

16 = 2 x 2 x 4 = 2² x 4
20 = 2 x 2 x 5 = 2² x 5

НОК = 2² x 4  x 5 = 80

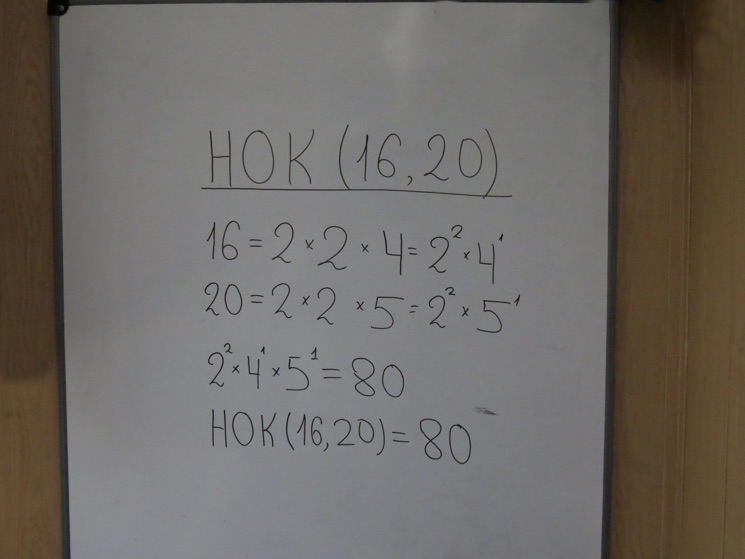
Ну и традиционно перейдем к практическому применению нахождения НОК.

Задача с применением НОК

Из Автовокзала в Севастополе одновременно отходят два автобуса по разным маршрутам. Первой автобус Мерседес путь в Краснодар и обратно проедет за 16 часов, а второй автобус Икарус в Анапу и обратно проедет маршрут за 20 часов. Время на остановки в пунктах отправления и прибытия одинаковое и уже включено в условные 16 и 20 часов. Условия их следование непрерывное.

Решение. Выезжая из Севастополя два автобуса следуют по разным маршрутам и вернуться в точку отправления в разное время. Когда автобус Икарус вернется из Анапы, автобус Мерседес уже второй раз выйдет из Севастополя и будет снова в пути. Эти автобусы с какой-то периодичностью во времени встретятся снова в Севастополе. И для того, чтобы узнать через какой время они встретятся необходимо найти наименьшее общее кратное. Воспользовавшись правилом вычисления НОК, приведенным выше, мы получаем время их встречи через 80 часов.

Вот мы снова убедились, что подобное правило имеет право на практическое применение в жизни. Если у вас есть свои практические задачи на нахождения НОК, то вы их можете оставить в комментариях и мы их включим обязательно в публикацию.